Continuing the series:
What is better to store hierarchical data: nested sets model or adjacency list (parent-child) model?
For detailed explanations of the terms, see the first article in the series:
This is the last article of the series which covers MySQL.
MySQL differs from the other systems, since it is the only system of the big four that does not support recursion natively. It has neither recursive CTE's nor CONNECT BY clause, not even rowset returning functions that help to emulate recursion in PostgreSQL 8.3.
MySQL supports a thing that all other systems either lack or implement inefficiently: session variables. They can be set in a SELECT clause and can be used to keep some kind of a state between the rows as they are processed and returned in a rowset.
This of course is against the whole spirit of SQL, since SQL implies operations on whole sets and session variables operate on rows and are totally dependent on the order they are returned or processed. But if used properly, this behavior can be exploited to emulate some things that MySQL lacks: analytic functions, efficient random row sampling etc.
Hierarchical functions are among the things that need to be emulated in MySQL using session variables to keep the function state.
Here's the old article in my blog that shows how to do this:
On the other hand, MySQL implements one more thing that is useful for nested sets model: SPATIAL indexes.
Spatial indexes and nested sets model
Unlike most other systems, MySQL allows creating indexes of different types, one of them being SPATIAL.
A spatial index is an R-Tree structure that allows indexing multidimensional values (though MySQL only indexes two-dimensional ones). Each value is represented by its minimal bounding box (minimal rectangle that contains the whole shape), and this is what is stored in the index.
The index allows to find an answer efficiently to the following question: given a point, what are the boxes that contain it?
Though this type of query is commonly used on geometrical or geographical data, like find all public toilets within 100 meters of my current location and for God's sake don't make it a fullscan
. However, this index can be used on any type of query that requires searching a given point in a range defined by two columns just as well.
A plain B-Tree index is good for range queries: find all values within the range defined by two boundaries
, like shown on this picture:
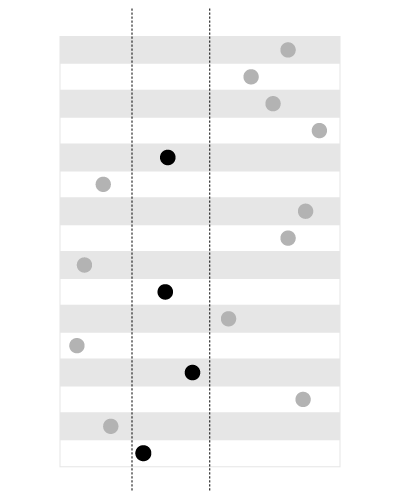
Black dots show values that fall inside the range (defined with two constant boundaries). It's easy to find these values if they are sorted: all values will make a contiguous block. That's what exactly the B-Tree index do: sort the values and return contiguous blocks.
But if we need to find variable ranges containing a constant point, like on this picture:
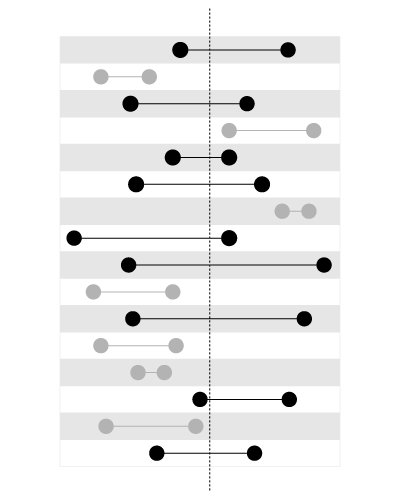
, a B-Tree index won't help, since we have two values here which we just cannot sort using one sort order. An R-Tree index, on the contrary, is perfect for this type of query.
Tasks requiring seaching for a value inside a known range are very common, that's why almost all database management systems provide a way to build and use a B-Tree index.
There is also a certain class of tasks that require searching for all ranges containing a known value:
and several others. These tasks can be improved by using R-Tree capabilities of MySQL:
The nested sets model belongs to both classes of tasks. It requires the first query (find variable values within a constant range) to build the list of descendants, and the second query (find variable ranges that contain a constant value) to build the list of ancestors.
That's exactly why it's so fast on building the list of descendants and so slow on building the list of ancestors.
Using an R-Tree index, nested sets model can be improved.
MySQL can only create an R-Tree index on a GEOMETRY type in a MyISAM table and use it in two special predicates, MBRContains and MBRWithin.
We should represent out nested sets boundaries (lft, rgt) as a LineString(Point(-1, lft), Point(1, rgt)), and search for a Point(0, value) using any of the predicates above.
This is not much of a stretch, actually, from the logical point of view: the nested sets are usually graphically represented as big boxes (parents) containing smaller boxes (children), and that's exactly what these predicates are designed for: searching for a boxes containing other boxes.
Let's create a sample table:
Table creation script
CREATE TABLE filler (
id INT NOT NULL PRIMARY KEY AUTO_INCREMENT
) ENGINE=Memory;
CREATE TABLE t_hierarchy (
id INT NOT NULL PRIMARY KEY,
parent INT NOT NULL,
lft INT NOT NULL,
rgt INT NOT NULL,
sets LineString NOT NULL,
data VARCHAR(100) NOT NULL,
stuffing VARCHAR(100) NOT NULL
) ENGINE=MyISAM;
DELIMITER $$
CREATE PROCEDURE prc_filler(cnt INT)
BEGIN
DECLARE _cnt INT;
SET _cnt = 1;
WHILE _cnt <= cnt DO
INSERT
INTO filler
SELECT _cnt;
SET _cnt = _cnt + 1;
END WHILE;
END;
$$
CREATE PROCEDURE prc_hierarchy(width INT)
main:BEGIN
DECLARE last INT;
DECLARE level INT;
SET last = 0;
SET level = 0;
WHILE width >= 1 DO
INSERT
INTO t_hierarchy
SELECT COALESCE(h.id, 0) * 5 + f.id,
COALESCE(h.id, 0),
COALESCE(h.lft, 0) + 1 + (f.id - 1) * width,
COALESCE(h.lft, 0) + f.id * width,
LineString(
Point(-1, COALESCE(h.lft, 0) + 1 + (f.id - 1) * width),
Point(1, COALESCE(h.lft, 0) + f.id * width)
),
CONCAT('Value ', COALESCE(h.id, 0) * 5 + f.id),
RPAD('', 100, '*')
FROM filler f
LEFT JOIN
t_hierarchy h
ON h.id >= last;
SET width = width / 5;
SET last = last + POWER(5, level);
SET level = level + 1;
END WHILE;
END
$$
DELIMITER ;
START TRANSACTION;
CALL prc_filler(5);
CALL prc_hierarchy(585937);
COMMIT;
CREATE INDEX ix_hierarchy_parent ON t_hierarchy (parent);
CREATE INDEX ix_hierarchy_lft ON t_hierarchy (lft);
CREATE INDEX ix_hierarchy_rgt ON t_hierarchy (rgt);
CREATE SPATIAL INDEX sx_hierarchy_sets ON t_hierarchy (sets);
The table contains 8 levels of hierarchy, 5 children to each parent and 2,441,405 records. Hierarchical attributes are defined for both adjacency list model (parent) and nested sets model (lft, rgt). All these fields are indexed with plain B-Tree indexes.
The field sets represents the diagonal of the bounding box of each record. All children's boxes are contained within the parent box. This field is indexed with an R-Tree (SPATIAL) index.
To query the adjacency list, we also need to create a pair of special functions as described in the article about hierarchical queries in MySQL:
The hierarchical functions
CREATE FUNCTION hierarchy_connect_by_parent_eq_prior_id_with_level(value INT, maxlevel INT) RETURNS INT
NOT DETERMINISTIC
READS SQL DATA
BEGIN
DECLARE _id INT;
DECLARE _parent INT;
DECLARE _next INT;
DECLARE _i INT;
DECLARE CONTINUE HANDLER FOR NOT FOUND SET @id = NULL;
SET _parent = @id;
SET _id = -1;
SET _i = 0;
IF @id IS NULL THEN
RETURN NULL;
END IF;
LOOP
SELECT MIN(id)
INTO @id
FROM t_hierarchy
WHERE parent = _parent
AND id > _id
AND COALESCE(@level < maxlevel, TRUE);
IF @id IS NOT NULL OR _parent = @start_with THEN
SET @level = @level + 1;
RETURN @id;
END IF;
SET @level := @level - 1;
SELECT id, parent
INTO _id, _parent
FROM t_hierarchy
WHERE id = _parent;
SET _i = _i + 1;
END LOOP;
RETURN NULL;
END
$$
CREATE FUNCTION hierarchy_connect_by_parent_eq_prior_id(value INT) RETURNS INT
NOT DETERMINISTIC
READS SQL DATA
BEGIN
DECLARE _id INT;
DECLARE _parent INT;
DECLARE _next INT;
DECLARE CONTINUE HANDLER FOR NOT FOUND SET @id = NULL;
SET _parent = @id;
SET _id = -1;
IF @id IS NULL THEN
RETURN NULL;
END IF;
LOOP
SELECT MIN(id)
INTO @id
FROM t_hierarchy
WHERE parent = _parent
AND id > _id;
IF @id IS NOT NULL OR _parent = @start_with THEN
SET @level = @level + 1;
RETURN @id;
END IF;
SET @level := @level - 1;
SELECT id, parent
INTO _id, _parent
FROM t_hierarchy
WHERE id = _parent;
END LOOP;
END
$$
These functions are described in more detail in this and this article.
Now, let's run the queries.
All descendants
Nested sets
SELECT SUM(LENGTH(hc.stuffing))
FROM t_hierarchy hp
JOIN t_hierarchy hc
ON hc.lft BETWEEN hp.lft AND hp.rgt
WHERE hp.id = 42
We don't use any spatial columns or indexes here.
Since this query requiries searching for all records with values of lft lying within the given range (that between lft and rgt of the parent record), a plain B-Tree index on a plain INT column is just fine.
View query details
| SUM(LENGTH(hc.stuffing)) |
| 1953100 |
| 1 row fetched in 0.0001s (0.3055s) |
| id |
select_type |
table |
type |
possible_keys |
key |
key_len |
ref |
rows |
filtered |
Extra |
| 1 |
SIMPLE |
hp |
const |
PRIMARY,ix_hierarchy_lft,ix_hierarchy_rgt |
PRIMARY |
4 |
const |
1 |
100.00 |
|
| 1 |
SIMPLE |
hc |
range |
ix_hierarchy_lft |
ix_hierarchy_lft |
4 |
|
23548 |
100.00 |
Using where |
select sum(length(`20090929_nested`.`hc`.`stuffing`)) AS `SUM(LENGTH(hc.stuffing))` from `20090929_nested`.`t_hierarchy` `hp` join `20090929_nested`.`t_hierarchy` `hc` where ((`20090929_nested`.`hc`.`lft` between '257814' and '281250'))
The query completes in 300 ms.
Adjacency list
SELECT SUM(LENGTH(stuffing))
FROM (
SELECT 42 AS id
UNION ALL
SELECT hierarchy_connect_by_parent_eq_prior_id(id) AS id
FROM (
SELECT @start_with := 42,
@id := @start_with,
@level := 0
) vars, t_hierarchy
WHERE @id IS NOT NULL
) ho
JOIN t_hierarchy hi
ON hi.id = ho.id
Since MySQL does not support recursive queries natively, we use the function to iterate the trees and a set of session variables to maintain the state of the function between calls.
To provide the results as a resultset, we call the function it SELECT clause of a query over the table, disregarding the input parameters. The table in the FROM clause is used as a dummy rowsource.
View query details
| SUM(LENGTH(stuffing)) |
| 1953100 |
| 1 row fetched in 0.0001s (7.5325s) |
| id |
select_type |
table |
type |
possible_keys |
key |
key_len |
ref |
rows |
filtered |
Extra |
| 1 |
PRIMARY |
<derived2> |
ALL |
|
|
|
|
19532 |
100.00 |
|
| 1 |
PRIMARY |
hi |
eq_ref |
PRIMARY |
PRIMARY |
4 |
ho.id |
1 |
100.00 |
Using where |
| 2 |
DERIVED |
|
|
|
|
|
|
|
|
No tables used |
| 3 |
UNCACHEABLE UNION |
<derived4> |
system |
|
|
|
|
1 |
100.00 |
|
| 3 |
UNCACHEABLE UNION |
t_hierarchy |
index |
|
PRIMARY |
4 |
|
2441405 |
100.00 |
Using where; Using index |
| 4 |
DERIVED |
|
|
|
|
|
|
|
|
No tables used |
|
UNION RESULT |
<union2,3> |
ALL |
|
|
|
|
|
|
|
select sum(length(`20090929_nested`.`hi`.`stuffing`)) AS `SUM(LENGTH(stuffing))` from (select 42 AS `id` union all select `hierarchy_connect_by_parent_eq_prior_id`(`20090929_nested`.`t_hierarchy`.`id`) AS `id` from (select (@start_with:=42) AS `@start_with := 42`,(@id:=(@start_with)) AS `@id := @start_with`,(@level:=0) AS `@level := 0`) `vars` join `20090929_nested`.`t_hierarchy` where ((@id) is not null)) `ho` join `20090929_nested`.`t_hierarchy` `hi` where (`20090929_nested`.`hi`.`id` = `ho`.`id`)
This query runs for 7 seconds.
All ancestors
Nested sets
SELECT hp.id, hp.parent, hp.lft, hp.rgt, hp.data
FROM t_hierarchy hc
JOIN t_hierarchy hp
ON MBRWithin(Point(0, hc.lft), hp.sets)
WHERE hc.id = 1000000
ORDER BY
lft
This query uses the R-Tree index. To do that, we convert lft to a point with coordinates (0, lft) and search for all boxes containing this point using MBRWithin.
View query details
| id |
parent |
lft |
rgt |
data |
| 2 |
0 |
585938 |
1171874 |
Value 2 |
| 12 |
2 |
703126 |
820312 |
Value 12 |
| 63 |
12 |
750001 |
773437 |
Value 63 |
| 319 |
63 |
764063 |
768749 |
Value 319 |
| 1599 |
319 |
766875 |
767811 |
Value 1599 |
| 7999 |
1599 |
767437 |
767623 |
Value 7999 |
| 39999 |
7999 |
767549 |
767585 |
Value 39999 |
| 199999 |
39999 |
767571 |
767577 |
Value 199999 |
| 1000000 |
199999 |
767576 |
767576 |
Value 1000000 |
| 9 rows fetched in 0.0005s (0.0151s) |
| id |
select_type |
table |
type |
possible_keys |
key |
key_len |
ref |
rows |
filtered |
Extra |
| 1 |
SIMPLE |
hc |
const |
PRIMARY |
PRIMARY |
4 |
const |
1 |
100.00 |
Using filesort |
| 1 |
SIMPLE |
hp |
range |
sx_hierarchy_sets |
sx_hierarchy_sets |
34 |
|
1 |
100.00 |
Using where |
select `20090929_nested`.`hp`.`id` AS `id`,`20090929_nested`.`hp`.`parent` AS `parent`,`20090929_nested`.`hp`.`lft` AS `lft`,`20090929_nested`.`hp`.`rgt` AS `rgt`,`20090929_nested`.`hp`.`data` AS `data` from `20090929_nested`.`t_hierarchy` `hc` join `20090929_nested`.`t_hierarchy` `hp` where (within(point(0,'767576'),`20090929_nested`.`hp`.`sets`)) order by `20090929_nested`.`hp`.`lft`
The query completes in 15 ms. This result is by far faster than everything we saw before. The same queries issued by the other systems are not assisted or poorly assisted by B-Tree indexes, and usually this query is a matter of seconds.
Adjacency list
SELECT hp.id, hp.parent, hp.lft, hp.rgt, hp.data
FROM (
SELECT @r AS _id,
@level := @level + 1 AS level,
(
SELECT @r := NULLIF(parent, 0)
FROM t_hierarchy hn
WHERE id = _id
)
FROM (
SELECT @r := 1000000,
@level := 0
) vars,
t_hierarchy hc
WHERE @r IS NOT NULL
) hc
JOIN t_hierarchy hp
ON hp.id = hc._id
ORDER BY
level DESC
Not that we don't even use a function for this query.
Each record has only one parent, and id is a PRIMARY KEY, thus the ancestry chain can be represented as a linked list.
To iterate the linked list, we can use an approach describe in this article:
, which requires no function, just a correlated subquery.
View query details
| id |
parent |
lft |
rgt |
data |
| 2 |
0 |
585938 |
1171874 |
Value 2 |
| 12 |
2 |
703126 |
820312 |
Value 12 |
| 63 |
12 |
750001 |
773437 |
Value 63 |
| 319 |
63 |
764063 |
768749 |
Value 319 |
| 1599 |
319 |
766875 |
767811 |
Value 1599 |
| 7999 |
1599 |
767437 |
767623 |
Value 7999 |
| 39999 |
7999 |
767549 |
767585 |
Value 39999 |
| 199999 |
39999 |
767571 |
767577 |
Value 199999 |
| 1000000 |
199999 |
767576 |
767576 |
Value 1000000 |
| 9 rows fetched in 0.0006s (0.5937s) |
| id |
select_type |
table |
type |
possible_keys |
key |
key_len |
ref |
rows |
filtered |
Extra |
| 1 |
PRIMARY |
<derived2> |
ALL |
|
|
|
|
9 |
100.00 |
Using filesort |
| 1 |
PRIMARY |
hp |
eq_ref |
PRIMARY |
PRIMARY |
4 |
hc._id |
1 |
100.00 |
Using where |
| 2 |
DERIVED |
<derived4> |
system |
|
|
|
|
1 |
100.00 |
|
| 2 |
DERIVED |
hc |
index |
|
PRIMARY |
4 |
|
2441405 |
100.00 |
Using where; Using index |
| 4 |
DERIVED |
|
|
|
|
|
|
|
|
No tables used |
| 3 |
DEPENDENT SUBQUERY |
hn |
eq_ref |
PRIMARY |
PRIMARY |
4 |
func |
1 |
100.00 |
Using where |
Field or reference '_id' of SELECT #3 was resolved in SELECT #2
select `20090929_nested`.`hp`.`id` AS `id`,`20090929_nested`.`hp`.`parent` AS `parent`,`20090929_nested`.`hp`.`lft` AS `lft`,`20090929_nested`.`hp`.`rgt` AS `rgt`,`20090929_nested`.`hp`.`data` AS `data` from (select (@r) AS `_id`,(@level:=((@level) + 1)) AS `level`,(select (@r:=nullif(`20090929_nested`.`hn`.`parent`,0)) AS `@r := NULLIF(parent, 0)` from `20090929_nested`.`t_hierarchy` `hn` where (`20090929_nested`.`hn`.`id` = `_id`)) AS `(
SELECT @r := NULLIF(parent, 0)
FROM t_hierarchy hn
WHERE id = _id
)` from (select (@r:=1000000) AS `@r := 1000000`,(@level:=0) AS `@level := 0`) `vars` join `20090929_nested`.`t_hierarchy` `hc` where ((@r) is not null)) `hc` join `20090929_nested`.`t_hierarchy` `hp` where (`20090929_nested`.`hp`.`id` = `hc`.`_id`) order by `hc`.`level` desc
This query completes in 600 ms, which is much longer than the nested sets solution.
All descendants up to a certain level
Nested sets
SELECT hc.id, hc.parent, hc.lft, hc.rgt, hc.data
FROM t_hierarchy hp
JOIN t_hierarchy hc
ON hc.lft BETWEEN hp.lft AND hp.rgt
JOIN t_hierarchy hr
ON MBRWithin(Point(0, hc.lft), hr.sets)
WHERE hp.id = ?
GROUP BY
hc.id
HAVING COUNT(*) <=
(
SELECT COUNT(*)
FROM t_hierarchy hp
JOIN t_hierarchy hrp
ON MBRWithin(Point(0, hp.lft), hrp.sets)
WHERE hp.id = ?
) + 2
ORDER BY
hc.lft
This query is adjusted for better usage of the R-Tree indexes.
We find all descendents of the item in question and then calculate the total number of parents (which gives us the depth level of each of the children). Then we just compare it with the level of the item.
This solution depends on the number of item's children too, however, let's see the performance:
View query for item 42
SELECT hc.id, hc.parent, hc.lft, hc.rgt, hc.data
FROM t_hierarchy hp
JOIN t_hierarchy hc
ON hc.lft BETWEEN hp.lft AND hp.rgt
JOIN t_hierarchy hr
ON MBRWithin(Point(0, hc.lft), hr.sets)
WHERE hp.id = 42
GROUP BY
hc.id
HAVING COUNT(*) <=
(
SELECT COUNT(*)
FROM t_hierarchy hp
JOIN t_hierarchy hrp
ON MBRWithin(Point(0, hp.lft), hrp.sets)
WHERE hp.id = 42
) + 2
ORDER BY
hc.lft
| id |
parent |
lft |
rgt |
data |
| 42 |
8 |
257814 |
281250 |
Value 42 |
| 211 |
42 |
257815 |
262501 |
Value 211 |
| 1056 |
211 |
257816 |
258752 |
Value 1056 |
| 1057 |
211 |
258753 |
259689 |
Value 1057 |
| 1058 |
211 |
259690 |
260626 |
Value 1058 |
| 1059 |
211 |
260627 |
261563 |
Value 1059 |
| 1060 |
211 |
261564 |
262500 |
Value 1060 |
| 212 |
42 |
262502 |
267188 |
Value 212 |
| 1061 |
212 |
262503 |
263439 |
Value 1061 |
| 1062 |
212 |
263440 |
264376 |
Value 1062 |
| 1063 |
212 |
264377 |
265313 |
Value 1063 |
| 1064 |
212 |
265314 |
266250 |
Value 1064 |
| 1065 |
212 |
266251 |
267187 |
Value 1065 |
| 213 |
42 |
267189 |
271875 |
Value 213 |
| 1066 |
213 |
267190 |
268126 |
Value 1066 |
| 1067 |
213 |
268127 |
269063 |
Value 1067 |
| 1068 |
213 |
269064 |
270000 |
Value 1068 |
| 1069 |
213 |
270001 |
270937 |
Value 1069 |
| 1070 |
213 |
270938 |
271874 |
Value 1070 |
| 214 |
42 |
271876 |
276562 |
Value 214 |
| 1071 |
214 |
271877 |
272813 |
Value 1071 |
| 1072 |
214 |
272814 |
273750 |
Value 1072 |
| 1073 |
214 |
273751 |
274687 |
Value 1073 |
| 1074 |
214 |
274688 |
275624 |
Value 1074 |
| 1075 |
214 |
275625 |
276561 |
Value 1075 |
| 215 |
42 |
276563 |
281249 |
Value 215 |
| 1076 |
215 |
276564 |
277500 |
Value 1076 |
| 1077 |
215 |
277501 |
278437 |
Value 1077 |
| 1078 |
215 |
278438 |
279374 |
Value 1078 |
| 1079 |
215 |
279375 |
280311 |
Value 1079 |
| 1080 |
215 |
280312 |
281248 |
Value 1080 |
| 31 rows fetched in 0.0014s (4.8592s) |
| id |
select_type |
table |
type |
possible_keys |
key |
key_len |
ref |
rows |
filtered |
Extra |
| 1 |
PRIMARY |
hp |
const |
PRIMARY,ix_hierarchy_lft,ix_hierarchy_rgt |
PRIMARY |
4 |
const |
1 |
100.00 |
Using temporary; Using filesort |
| 1 |
PRIMARY |
hc |
range |
ix_hierarchy_lft |
ix_hierarchy_lft |
4 |
|
23548 |
100.00 |
Using where |
| 1 |
PRIMARY |
hr |
ALL |
sx_hierarchy_sets |
|
|
|
2441405 |
100.00 |
Range checked for each record (index map: 0x10) |
| 2 |
SUBQUERY |
hp |
const |
PRIMARY |
PRIMARY |
4 |
const |
1 |
100.00 |
|
| 2 |
SUBQUERY |
hrp |
range |
sx_hierarchy_sets |
sx_hierarchy_sets |
34 |
|
1 |
100.00 |
Using where |
select `20090929_nested`.`hc`.`id` AS `id`,`20090929_nested`.`hc`.`parent` AS `parent`,`20090929_nested`.`hc`.`lft` AS `lft`,`20090929_nested`.`hc`.`rgt` AS `rgt`,`20090929_nested`.`hc`.`data` AS `data` from `20090929_nested`.`t_hierarchy` `hp` join `20090929_nested`.`t_hierarchy` `hc` join `20090929_nested`.`t_hierarchy` `hr` where (within(point(0,`20090929_nested`.`hc`.`lft`),`20090929_nested`.`hr`.`sets`) and (`20090929_nested`.`hc`.`lft` between '257814' and '281250')) group by `20090929_nested`.`hc`.`id` having (count(0) <= ((select count(0) AS `COUNT(*)` from `20090929_nested`.`t_hierarchy` `hp` join `20090929_nested`.`t_hierarchy` `hrp` where (within(point(0,'257814'),`20090929_nested`.`hrp`.`sets`))) + 2)) order by `20090929_nested`.`hc`.`lft`
View query for item 42
SELECT hc.id, hc.parent, hc.lft, hc.rgt, hc.data
FROM t_hierarchy hp
JOIN t_hierarchy hc
ON hc.lft BETWEEN hp.lft AND hp.rgt
JOIN t_hierarchy hr
ON MBRWithin(Point(0, hc.lft), hr.sets)
WHERE hp.id = 31415
GROUP BY
hc.id
HAVING COUNT(*) <=
(
SELECT COUNT(*)
FROM t_hierarchy hp
JOIN t_hierarchy hrp
ON MBRWithin(Point(0, hp.lft), hrp.sets)
WHERE hp.id = 31415
) + 2
ORDER BY
hc.lft
| id |
parent |
lft |
rgt |
data |
| 31415 |
6282 |
445651 |
445687 |
Value 31415 |
| 157076 |
31415 |
445652 |
445658 |
Value 157076 |
| 785381 |
157076 |
445653 |
445653 |
Value 785381 |
| 785382 |
157076 |
445654 |
445654 |
Value 785382 |
| 785383 |
157076 |
445655 |
445655 |
Value 785383 |
| 785384 |
157076 |
445656 |
445656 |
Value 785384 |
| 785385 |
157076 |
445657 |
445657 |
Value 785385 |
| 157077 |
31415 |
445659 |
445665 |
Value 157077 |
| 785386 |
157077 |
445660 |
445660 |
Value 785386 |
| 785387 |
157077 |
445661 |
445661 |
Value 785387 |
| 785388 |
157077 |
445662 |
445662 |
Value 785388 |
| 785389 |
157077 |
445663 |
445663 |
Value 785389 |
| 785390 |
157077 |
445664 |
445664 |
Value 785390 |
| 157078 |
31415 |
445666 |
445672 |
Value 157078 |
| 785391 |
157078 |
445667 |
445667 |
Value 785391 |
| 785392 |
157078 |
445668 |
445668 |
Value 785392 |
| 785393 |
157078 |
445669 |
445669 |
Value 785393 |
| 785394 |
157078 |
445670 |
445670 |
Value 785394 |
| 785395 |
157078 |
445671 |
445671 |
Value 785395 |
| 157079 |
31415 |
445673 |
445679 |
Value 157079 |
| 785396 |
157079 |
445674 |
445674 |
Value 785396 |
| 785397 |
157079 |
445675 |
445675 |
Value 785397 |
| 785398 |
157079 |
445676 |
445676 |
Value 785398 |
| 785399 |
157079 |
445677 |
445677 |
Value 785399 |
| 785400 |
157079 |
445678 |
445678 |
Value 785400 |
| 157080 |
31415 |
445680 |
445686 |
Value 157080 |
| 785401 |
157080 |
445681 |
445681 |
Value 785401 |
| 785402 |
157080 |
445682 |
445682 |
Value 785402 |
| 785403 |
157080 |
445683 |
445683 |
Value 785403 |
| 785404 |
157080 |
445684 |
445684 |
Value 785404 |
| 785405 |
157080 |
445685 |
445685 |
Value 785405 |
| 31 rows fetched in 0.0014s (0.0105s) |
| id |
select_type |
table |
type |
possible_keys |
key |
key_len |
ref |
rows |
filtered |
Extra |
| 1 |
PRIMARY |
hp |
const |
PRIMARY,ix_hierarchy_lft,ix_hierarchy_rgt |
PRIMARY |
4 |
const |
1 |
100.00 |
Using temporary; Using filesort |
| 1 |
PRIMARY |
hc |
range |
ix_hierarchy_lft |
ix_hierarchy_lft |
4 |
|
28 |
100.00 |
Using where |
| 1 |
PRIMARY |
hr |
ALL |
sx_hierarchy_sets |
|
|
|
2441405 |
100.00 |
Range checked for each record (index map: 0x10) |
| 2 |
SUBQUERY |
hp |
const |
PRIMARY |
PRIMARY |
4 |
const |
1 |
100.00 |
|
| 2 |
SUBQUERY |
hrp |
range |
sx_hierarchy_sets |
sx_hierarchy_sets |
34 |
|
1 |
100.00 |
Using where |
select `20090929_nested`.`hc`.`id` AS `id`,`20090929_nested`.`hc`.`parent` AS `parent`,`20090929_nested`.`hc`.`lft` AS `lft`,`20090929_nested`.`hc`.`rgt` AS `rgt`,`20090929_nested`.`hc`.`data` AS `data` from `20090929_nested`.`t_hierarchy` `hp` join `20090929_nested`.`t_hierarchy` `hc` join `20090929_nested`.`t_hierarchy` `hr` where (within(point(0,`20090929_nested`.`hc`.`lft`),`20090929_nested`.`hr`.`sets`) and (`20090929_nested`.`hc`.`lft` between '445651' and '445687')) group by `20090929_nested`.`hc`.`id` having (count(0) <= ((select count(0) AS `COUNT(*)` from `20090929_nested`.`t_hierarchy` `hp` join `20090929_nested`.`t_hierarchy` `hrp` where (within(point(0,'445651'),`20090929_nested`.`hrp`.`sets`))) + 2)) order by `20090929_nested`.`hc`.`lft`
The query for item 42 (which has about 20,000 descendants) took minutes in the other systems. Now it completes in less than 5 seconds.
The same query for item 31,415 is over in just 10 ms.
Adjacency list
SELECT hi.id, hi.parent, hi.lft, hi.rgt, hi.data
FROM (
SELECT ? AS id
UNION ALL
SELECT hierarchy_connect_by_parent_eq_prior_id_with_level(id, 2) AS id
FROM (
SELECT @start_with := ?,
@id := @start_with,
@level := 0
) vars, t_hierarchy
WHERE @id IS NOT NULL
) ho
JOIN t_hierarchy hi
ON hi.id = ho.id
This query imitates recursion, so performance does not directly depend on the number of descendants.
View query for item 42
SELECT hi.id, hi.parent, hi.lft, hi.rgt, hi.data
FROM (
SELECT 42 AS id
UNION ALL
SELECT hierarchy_connect_by_parent_eq_prior_id_with_level(id, 2) AS id
FROM (
SELECT @start_with := 42,
@id := @start_with,
@level := 0
) vars, t_hierarchy
WHERE @id IS NOT NULL
) ho
JOIN t_hierarchy hi
ON hi.id = ho.id
| id |
parent |
lft |
rgt |
data |
| 42 |
8 |
257814 |
281250 |
Value 42 |
| 211 |
42 |
257815 |
262501 |
Value 211 |
| 1056 |
211 |
257816 |
258752 |
Value 1056 |
| 1057 |
211 |
258753 |
259689 |
Value 1057 |
| 1058 |
211 |
259690 |
260626 |
Value 1058 |
| 1059 |
211 |
260627 |
261563 |
Value 1059 |
| 1060 |
211 |
261564 |
262500 |
Value 1060 |
| 212 |
42 |
262502 |
267188 |
Value 212 |
| 1061 |
212 |
262503 |
263439 |
Value 1061 |
| 1062 |
212 |
263440 |
264376 |
Value 1062 |
| 1063 |
212 |
264377 |
265313 |
Value 1063 |
| 1064 |
212 |
265314 |
266250 |
Value 1064 |
| 1065 |
212 |
266251 |
267187 |
Value 1065 |
| 213 |
42 |
267189 |
271875 |
Value 213 |
| 1066 |
213 |
267190 |
268126 |
Value 1066 |
| 1067 |
213 |
268127 |
269063 |
Value 1067 |
| 1068 |
213 |
269064 |
270000 |
Value 1068 |
| 1069 |
213 |
270001 |
270937 |
Value 1069 |
| 1070 |
213 |
270938 |
271874 |
Value 1070 |
| 214 |
42 |
271876 |
276562 |
Value 214 |
| 1071 |
214 |
271877 |
272813 |
Value 1071 |
| 1072 |
214 |
272814 |
273750 |
Value 1072 |
| 1073 |
214 |
273751 |
274687 |
Value 1073 |
| 1074 |
214 |
274688 |
275624 |
Value 1074 |
| 1075 |
214 |
275625 |
276561 |
Value 1075 |
| 215 |
42 |
276563 |
281249 |
Value 215 |
| 1076 |
215 |
276564 |
277500 |
Value 1076 |
| 1077 |
215 |
277501 |
278437 |
Value 1077 |
| 1078 |
215 |
278438 |
279374 |
Value 1078 |
| 1079 |
215 |
279375 |
280311 |
Value 1079 |
| 1080 |
215 |
280312 |
281248 |
Value 1080 |
| 31 rows fetched in 0.0013s (0.6250s) |
| id |
select_type |
table |
type |
possible_keys |
key |
key_len |
ref |
rows |
filtered |
Extra |
| 1 |
PRIMARY |
<derived2> |
ALL |
|
|
|
|
32 |
100.00 |
|
| 1 |
PRIMARY |
hi |
eq_ref |
PRIMARY |
PRIMARY |
4 |
ho.id |
1 |
100.00 |
Using where |
| 2 |
DERIVED |
|
|
|
|
|
|
|
|
No tables used |
| 3 |
UNCACHEABLE UNION |
<derived4> |
system |
|
|
|
|
1 |
100.00 |
|
| 3 |
UNCACHEABLE UNION |
t_hierarchy |
index |
|
PRIMARY |
4 |
|
2441405 |
100.00 |
Using where; Using index |
| 4 |
DERIVED |
|
|
|
|
|
|
|
|
No tables used |
|
UNION RESULT |
<union2,3> |
ALL |
|
|
|
|
|
|
|
select `20090929_nested`.`hi`.`id` AS `id`,`20090929_nested`.`hi`.`parent` AS `parent`,`20090929_nested`.`hi`.`lft` AS `lft`,`20090929_nested`.`hi`.`rgt` AS `rgt`,`20090929_nested`.`hi`.`data` AS `data` from (select 42 AS `id` union all select `hierarchy_connect_by_parent_eq_prior_id_with_level`(`20090929_nested`.`t_hierarchy`.`id`,2) AS `id` from (select (@start_with:=42) AS `@start_with := 42`,(@id:=(@start_with)) AS `@id := @start_with`,(@level:=0) AS `@level := 0`) `vars` join `20090929_nested`.`t_hierarchy` where ((@id) is not null)) `ho` join `20090929_nested`.`t_hierarchy` `hi` where (`20090929_nested`.`hi`.`id` = `ho`.`id`)
View query for item 31,415
SELECT hi.id, hi.parent, hi.lft, hi.rgt, hi.data
FROM (
SELECT 31415 AS id
UNION ALL
SELECT hierarchy_connect_by_parent_eq_prior_id_with_level(id, 2) AS id
FROM (
SELECT @start_with := 31415,
@id := @start_with,
@level := 0
) vars, t_hierarchy
WHERE @id IS NOT NULL
) ho
JOIN t_hierarchy hi
ON hi.id = ho.id
| id |
parent |
lft |
rgt |
data |
| 31415 |
6282 |
445651 |
445687 |
Value 31415 |
| 157076 |
31415 |
445652 |
445658 |
Value 157076 |
| 785381 |
157076 |
445653 |
445653 |
Value 785381 |
| 785382 |
157076 |
445654 |
445654 |
Value 785382 |
| 785383 |
157076 |
445655 |
445655 |
Value 785383 |
| 785384 |
157076 |
445656 |
445656 |
Value 785384 |
| 785385 |
157076 |
445657 |
445657 |
Value 785385 |
| 157077 |
31415 |
445659 |
445665 |
Value 157077 |
| 785386 |
157077 |
445660 |
445660 |
Value 785386 |
| 785387 |
157077 |
445661 |
445661 |
Value 785387 |
| 785388 |
157077 |
445662 |
445662 |
Value 785388 |
| 785389 |
157077 |
445663 |
445663 |
Value 785389 |
| 785390 |
157077 |
445664 |
445664 |
Value 785390 |
| 157078 |
31415 |
445666 |
445672 |
Value 157078 |
| 785391 |
157078 |
445667 |
445667 |
Value 785391 |
| 785392 |
157078 |
445668 |
445668 |
Value 785392 |
| 785393 |
157078 |
445669 |
445669 |
Value 785393 |
| 785394 |
157078 |
445670 |
445670 |
Value 785394 |
| 785395 |
157078 |
445671 |
445671 |
Value 785395 |
| 157079 |
31415 |
445673 |
445679 |
Value 157079 |
| 785396 |
157079 |
445674 |
445674 |
Value 785396 |
| 785397 |
157079 |
445675 |
445675 |
Value 785397 |
| 785398 |
157079 |
445676 |
445676 |
Value 785398 |
| 785399 |
157079 |
445677 |
445677 |
Value 785399 |
| 785400 |
157079 |
445678 |
445678 |
Value 785400 |
| 157080 |
31415 |
445680 |
445686 |
Value 157080 |
| 785401 |
157080 |
445681 |
445681 |
Value 785401 |
| 785402 |
157080 |
445682 |
445682 |
Value 785402 |
| 785403 |
157080 |
445683 |
445683 |
Value 785403 |
| 785404 |
157080 |
445684 |
445684 |
Value 785404 |
| 785405 |
157080 |
445685 |
445685 |
Value 785405 |
| 31 rows fetched in 0.0014s (0.6406s) |
| id |
select_type |
table |
type |
possible_keys |
key |
key_len |
ref |
rows |
filtered |
Extra |
| 1 |
PRIMARY |
<derived2> |
ALL |
|
|
|
|
32 |
100.00 |
|
| 1 |
PRIMARY |
hi |
eq_ref |
PRIMARY |
PRIMARY |
4 |
ho.id |
1 |
100.00 |
Using where |
| 2 |
DERIVED |
|
|
|
|
|
|
|
|
No tables used |
| 3 |
UNCACHEABLE UNION |
<derived4> |
system |
|
|
|
|
1 |
100.00 |
|
| 3 |
UNCACHEABLE UNION |
t_hierarchy |
index |
|
PRIMARY |
4 |
|
2441405 |
100.00 |
Using where; Using index |
| 4 |
DERIVED |
|
|
|
|
|
|
|
|
No tables used |
|
UNION RESULT |
<union2,3> |
ALL |
|
|
|
|
|
|
|
select `20090929_nested`.`hi`.`id` AS `id`,`20090929_nested`.`hi`.`parent` AS `parent`,`20090929_nested`.`hi`.`lft` AS `lft`,`20090929_nested`.`hi`.`rgt` AS `rgt`,`20090929_nested`.`hi`.`data` AS `data` from (select 31415 AS `id` union all select `hierarchy_connect_by_parent_eq_prior_id_with_level`(`20090929_nested`.`t_hierarchy`.`id`,2) AS `id` from (select (@start_with:=31415) AS `@start_with := 31415`,(@id:=(@start_with)) AS `@id := @start_with`,(@level:=0) AS `@level := 0`) `vars` join `20090929_nested`.`t_hierarchy` where ((@id) is not null)) `ho` join `20090929_nested`.`t_hierarchy` `hi` where (`20090929_nested`.`hi`.`id` = `ho`.`id`)
Both queries complete in 600 ms
Summary
MySQL differs from the other systems in its possibilities to handle hierarchical data.
On one hand, it lacks a native way to do recursive queries which makes traversing the hierarchy trees harder. It can be emulated using a custom function and session variables to maintain the recursion stack, but this solution is more slow.
On the other hand, MySQL supports R-Tree indexes which can be used to query the ranges containing a given value. This type of search is required for the nested sets queries and R-Tree index is faster.
However, adjacency list is still faster for retrieving all descendants up to the given level.
Both adjacency lists and nested sets require extra maintenance in MySQL: adjacency lists require building a custom function to query each table, nested sets require a function to update it.
Updating a nested sets model can be slow too since R-Tree indexes take much longer time to add to them than B-Tree indexes.
However, using R-Tree indexes, nested sets model is extra fast for searching for all descendants and all ancestors, and shows decent performance in determining the item's levels and filtering on them.
In MySQL, it is advisable to add the level column into the nested sets model which will make it super fast for all three types of queries. However, this will make it even more harder to update.
It should also be noted that the only storage engine that allows R-Tree indexes is MyISAM. In case of an update (which can affect millions of rows even to insert a single record), all table will be locked and will not be able to be queried.
Conclusion
In MySQL, the nested sets model should be preferred if the updates to the hierarhical structure are infrequent and it is affordable to lock the table for the duration of an update (which can take minutes on a long table).
This implies creating the table using MyISAM storage engine, creating the bounding box of a GEOMETRY type as described above, indexing it with a SPATIAL index and persisting the level in the table.
If the updates to the table are frequent or it is inaffordable to lock the table for a long period of time implied by an update, then the adjacency list model should be used to store the hierarchical data.
This requires creating a function to query the table.
MySQL is the only system of the big four (MySQL, Oracle, SQL Server, PostgreSQL) for which the nested sets model shows decent performance and can be considered to stored hierarchical data.


 Subscribe in a reader
Subscribe in a reader
“find all public toilets within 100 meters of my current location and for God’s sake don’t make it a fullscan”
that made me laugh out loud this morning – thank you :)
Gene
15 Oct 12 at 14:09
Ooh, thanks for the tip about using an R-tree index to speed up the nested set ancestor queries.
Annie
13 Jan 13 at 11:23
Other databases have spatial indexes as well… wouldn’t they be able to use the nested sets just as effectively as MySQL, or is there something magical about MyISAM’s R-Tree indexing?
Christopher Smith
16 Jan 13 at 23:06
@ChristopherSmith: of course they would. SQL Server and PostgreSQL, however, don’t implement their spatial indexes as R-Tree.
Quassnoi
17 Jan 13 at 02:29
Interesting.
But MyISAM doesn’t support transactions, so what’s the point of the transaction commands?
Peter Brawley
9 Aug 13 at 01:32
@Peter: I just copy and paste those scripts from post to post, changing them as needed.
Quassnoi
9 Aug 13 at 13:12
Thanks for sharing your scripts and test results. Very useful! Would be interesting to see the numbers for InnoDB.
Daniel
23 Oct 13 at 17:35
Thank you so much, for applied knowledgeable examples how to implement MySQL spatial data type toward hierarchical model.
WEB is full of posts recycling same examples with “electronics sht” without unveiling applied basics of how properly define and build these indexes in MySQL properly and thus taking model’s usage to its full potential strength.
Finally, here, straight and forward post how to translate integer position index to it’s geometrical interpretation required by a model.
Thanks so much again!
Misha Dar
4 Nov 14 at 23:29
This is a great series of articles, thank you. It was a pleasure to read them even as just a hobbyist.
But I’ve found that MyISAM doesn’t support foreign keys. So (if I’m not mistaken) I have to make a choice: either I have InnoDB tables and foreign keys or MyISAM tables and no foreign keys. Now, I have a hierarchy with only about 100 elements (and it won’t ever go over 200), so lookup is very fast even without a spatial index. If I’d like to keep foreign keys for integrity, may I opt to not use spatial indexes or are there any other reasons for using them besides lookup speed?
Péter Wolf
8 Jan 16 at 22:25
@Quassnoi, I’m sorry I didn’t notice your reply until now.
PostgreSQL absolutely does R-Tree indexes: https://www.postgresql.org/docs/8.1/static/indexes-types.html
Christopher Smith
24 Apr 17 at 20:36
@Christopher: I remember 2006, it was a nice year: I got married, found a good job, took alpine skiing. Unfortunately, some sad stuff also happened that year: my brother-in-law divorced, my parents’ cat died and PostgreSQL dropped R-Tree support.
Quassnoi
24 Apr 17 at 20:57
@Quassnoi R-Tree’s were migrated over to the GiST subsystem, and they’re still there as SP-GiST. It’s nice because SP-GiST supports a more flexible set of spatial indexing techniques.
Christopher Smith
24 Apr 17 at 21:32
@Christopher: of course, and that’s why I wrote PostgreSQL did not implement its spatial indexes using R-Tree. PostgreSQL does implement spatial indexing of course, it just does not do it using R-Tree.
Quassnoi
24 Apr 17 at 21:43
MySQL 8.0 (and MariaDB 10.2) do have Recursive CTEs.
Rick James
20 Jul 19 at 03:29
From what I can see in the MySQL docs, both MyISAM *and* InnoDB now supports SPATIAL and R-tree indexes.
Yan Wong
9 May 21 at 18:16